In the world of ray optics, understanding focal length is essential for anyone interested in how lenses work. The formula for determining the focal length (f) relates the refractive index (n) of the lens material and the radii of curvature (R1 and R2) of its surfaces. This formula is expressed as 1/f = (n – 1) × (1/R1 – 1/R2). This formula illustrates how the design and material of a lens can significantly affect its ability to focus light.
Lenses play a crucial role in various optical devices, from cameras to eyeglasses. By grasping the focal length concept, one can better appreciate how light behaves when passing through different lenses. This understanding is vital for anyone who wants to explore the broader field of optics, as it lays the groundwork for various applications and advancements.
Exploring the focal length in ray optics not only unveils the mechanics of lenses but also opens the door to many intriguing optical phenomena. As readers delve further into this topic, they will uncover how these principles manifest in everyday objects and technologies.
Fundamental Concepts of Ray Optics

Ray optics is crucial for understanding how light behaves when it encounters different mediums and how optical devices such as lenses manipulate light. This section explains the nature of light, the various types of lenses, and the formulas used to determine focal length.
Nature of Light and Refraction
Light travels in straight lines as rays until it hits a different medium, such as air or glass. This change in medium causes refraction, which is the bending of light. Snell’s Law mathematically describes this phenomenon, stating that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant, depending on the refractive indices of the two media.
When light enters a medium with a higher refractive index, it slows down and bends toward the normal line. Conversely, when it exits to a medium with a lower refractive index, it speeds up and bends away from the normal. Understanding these principles is essential for studying how lenses and mirrors form images.
Lenses and Their Types
Lenses are transparent optical devices that refract light to form images. The two main types of lenses are convex and concave.
A convex lens is thicker in the center and converges light rays to a focal point, while a concave lens is thinner in the center and diverges light rays.
Convex lenses are commonly used in magnifying glasses and cameras, while concave lenses are used in instruments like glasses for nearsightedness. The spherical shape of these lenses allows for a specific radius of curvature, which impacts the lens’s focusing ability. Understanding these types helps in practical applications like photography and vision correction.
Focal Length and Lens Formula
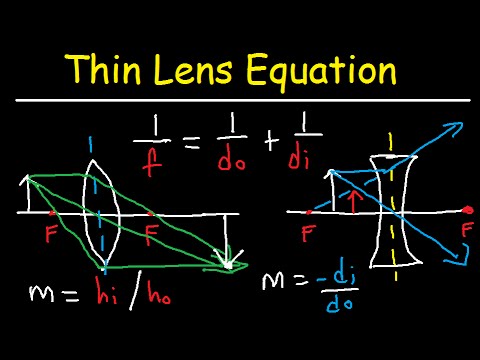
Focal length is the distance from the lens’s center to the focal point, where light converges or appears to diverge. The lens formula, given by 1/f = 1/do + 1/di, helps determine the relationship between the object distance (do), the image distance (di), and the focal length (f).
For mirrors, a similar formula applies: 1/f = 1/do + 1/di. These formulas are essential in ray tracing, which involves drawing light rays to predict the location and size of the image formed. The Lens Maker’s Formula is another important equation, expressed as 1/f = (n-1) × (1/R1 – 1/R2), where n is the lens’s refractive index and R1 and R2 are the radii of curvature of the two lens surfaces. Understanding these formulas is crucial for designing optical systems effectively.
Applications and Implications of Focal Length
Focal length plays a significant role in various fields of optics, especially in image formation and the design of optical instruments. Understanding its implications can improve the functionality of devices like microscopes and telescopes, as well as enhance the human eye’s ability to focus on objects.
Image Formation and Magnification
Focal length directly influences image formation. When light rays pass through a lens, they converge or diverge based on its focal length.
A shorter focal length creates a wider field of view, essential for capturing larger images. In contrast, a longer focal length provides higher magnification, making distant objects appear closer.
This property is vital in devices like the microscope, where it produces real images that can be viewed on a screen or eyepiece. Additionally, the image formed can be real and inverted, or virtual and upright, depending on the arrangement of the object relative to the lens’s focal point.
Optical Instruments and Human Eye
Focal length plays a critical role in the design of optical instruments such as telescopes, microscopes, and cameras.
In a compound microscope, the objective lens has a short focal length for high magnification, while the eyepiece lens further enlarges the image. This design allows for clearer viewing of tiny specimens.
The human eye operates similarly, with its focal length adjusting through the lens to focus on objects at varying distances. This adjustment ensures that light rays converge correctly on the retina, creating a clear image. Any issues in this process can lead to refractive errors that may require corrective lenses, which are designed based on specific focal lengths.
Power of the Lens and Practical Considerations
The power of a lens is inversely related to its focal length, measured in diopters.
A lens with a short focal length has high optical power, making it suitable for magnifying images, while a longer focal length lens has lower power for viewing distant objects.
Practical applications include the use of prisms and optical fiber where adjustments to focal length can influence behaviors like total internal reflection.
This aspect is especially useful in designing lenses for binoculars and other viewing instruments, optimizing their performance for different environments and uses.
Understanding these principles is crucial in manufacturing efficient optical devices.
