In the study of optics, understanding how light interacts with different materials involves key concepts such as the angle of incidence and the angle of refraction.
When a ray of light strikes a surface, it approaches at a specific angle known as the angle of incidence. This angle is measured from an imaginary line called the normal, which is perpendicular to the surface at the point of contact.
The angle of refraction occurs when the light passes into another medium and bends, changing its direction. The relationship between these two angles is crucial in various applications, including lenses, prisms, and fiber optics.
By analyzing both angles, one can gain insights into how light behaves when transitioning from one material to another.
Exploring the differences between the angle of incidence and the angle of refraction helps in understanding fundamental optical principles. This knowledge not only enriches scientific comprehension but also enhances practical applications in technology and photography.
Fundamentals of Light Behavior
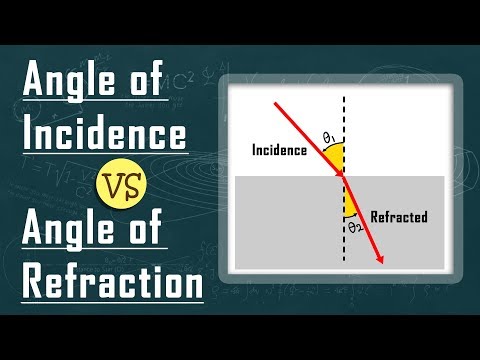
Light behaves in specific ways when it passes through different materials. Understanding these behaviors is key to grasping how light interacts with various media.
Two important concepts are the angle of incidence and the angle of refraction, which describe how light bends as it moves between different substances.
Understanding Refraction
Refraction occurs when light travels from one medium to another. The change in speed causes the light to bend at the boundary between these two media.
For example, when light moves from air into water, it slows down and bends towards the normal line, an imaginary perpendicular line at the boundary. The degree of bending depends on the characteristics of each medium.
Refraction is responsible for many optical effects, such as the distortion of objects underwater. Choosing the right material for lenses and glasses hinges on understanding these principles.
Roles of Angle of Incidence and Refraction
The angle of incidence is the angle between the incident ray of light and the normal line. When light hits the boundary, the angle of refraction forms with the normal as the light exits into a new medium.
Using Snell’s Law, the relationship between these angles can be calculated. If the angle of incidence is greater, the refraction angle can also vary.
For instance, with a larger angle, the light may bend more dramatically, moving faster in the second medium. This process plays a crucial role in optics, affecting everything from how we see images in a camera to the design of corrective lenses.
Optical Principles and Laws

Understanding how light behaves as it travels through different media is essential in optics. Key principles like Snell’s Law, the distinction between reflection and refraction, and phenomena like total internal reflection are fundamental.
Exploring Snell’s Law
Snell’s Law describes how light bends when it passes from one medium into another. The law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant. This constant is related to the refractive indices of the two media involved.
Mathematically, it is expressed as:
n1 * sin(θ1) = n2 * sin(θ2)
Here, n1 and n2 are the refractive indices, while θ1 and θ2 are the angles of incidence and refraction, respectively.
According to this law, when light moves from air to water, it slows down and bends toward the normal. This bending allows applications in lenses and prisms, crucial for optics.
Reflection Versus Refraction
When light strikes a surface, it can either reflect or refract. Reflection occurs when light bounces off a surface, following the law of reflection, which states that the angle of incidence equals the angle of reflection.
In contrast, refraction involves the bending of light as it enters a different medium. This bending is influenced by the medium’s refractive index.
For instance, when light travels from air (n ≈ 1.0003) into water (n ≈ 1.333), it slows down and bends.
The combination of these processes allows for a variety of visual effects and is essential in designing optical devices.
Total Internal Reflection and Critical Angle
Total internal reflection occurs when light travels from a denser medium to a less dense one at an angle greater than the critical angle. The critical angle is defined as the angle of incidence that results in an angle of refraction of 90 degrees.
Beyond this critical angle, all light is reflected back into the denser medium.
This principle is utilized in fiber optics, where light signals are guided over long distances without significant loss.
The critical angle can be calculated using Snell’s Law:
sin(θc) = n2/n1
Where θc is the critical angle. This phenomenon is crucial in telecommunications and imaging technologies, providing efficient ways to transmit light.
Measuring and Calculating Angles in Optics

Understanding how to measure and calculate angles is crucial in optics. The techniques used include tools like protractors and mathematical formulas that relate the different angles when light passes through various media.
Using a Protractor in Optics
A protractor is an essential tool for measuring angles in optical experiments. It helps determine the angle of incidence and the angle of refraction when a light ray hits a surface.
To use a protractor:
- Position the Protractor: Align the center hole with the point where the light ray hits the surface.
- Mark the Angles: Identify the angle of incidence (the angle between the incoming light ray and the normal line) and the angle of refraction (the angle between the refracted ray and the normal).
The readings can be read in degrees. Accurate measurements are critical for calculations involving the index of refraction.
Calculating the Index of Refraction
The index of refraction (n) is a key concept in optics, defining how light travels through a material. To calculate it, Snell’s Law is used, expressed mathematically as:
[ n = \frac{\sin(\Theta_i)}{\sin(\Theta_r)} ]
Here, ( \Theta_i ) is the angle of incidence, and ( \Theta_r ) is the angle of refraction.
The index of refraction provides insights into how light bends when entering different materials.
For instance, air has an index of approximately 1, while water has an index of about 1.33. Knowing the refractive indices helps in understanding light behavior in various situations.
Mathematical Relationship Between Angles
The relationship between the angle of incidence and the angle of refraction is fundamental in optics. According to Snell’s Law, this relationship can be expressed as:
[ n_1 \sin(\Theta_i) = n_2 \sin(\Theta_r) ]
In this equation, ( n_1 ) and ( n_2 ) represent the refractive indices of the two media.
When light travels from one medium to another, understanding this relationship allows scientists to predict how much light will bend. This bending is essential in designing lenses, optical fibers, and other optical devices.
Applications and Examples of Refraction

Refraction has many practical uses across different fields. It plays a key role in how light interacts with materials, leading to various applications in vision, communication, and scientific analysis.
Refraction in Lenses and Prisms
Lenses and prisms are everyday examples of refraction. Lenses bend light to focus or magnify images, enabling the functioning of glasses, cameras, and microscopes.
When light passes through a convex lens, it converges to a point, which is essential for clear vision. Conversely, a concave lens diverges light, causing images to appear smaller. Prisms, on the other hand, disperse light into its component colors. This occurs due to different wavelengths bending at different angles.
The bending of light in prisms demonstrates the relationship between the angle of incidence and the angle of refraction. This principle is fundamental in several optical devices like telescopes.
Fiber Optics and Telecommunications
Fiber optics utilize the principles of refraction for transmitting data. Light signals travel through thin strands of glass or plastic, allowing for fast and efficient communication.
In fiber optics, light reflects internally within the fiber, guided by the critical angle. This results in minimal loss of signal strength over long distances.
The refractive index of the materials used is vital since higher differences lead to better performance.
Fiber optics are widely used in internet and telephone networks, demonstrating how bending light facilitates modern communication.
Spectroscopy and Analysis
Spectroscopy is another important application of refraction. This technique involves studying the interaction between light and matter, which helps scientists analyze materials.
Different wavelengths of light can be refracted to provide valuable information about substances.
For example, the absorption and emission spectra indicate what elements are present in a sample.
Using refractive techniques, scientists can detect changes in speed as light moves through different substances, which is crucial in chemical analysis.
This method is essential in laboratories for identifying materials and understanding their properties.
