Abbe’s formula is a key concept in optics that relates to resolution in microscopy. It defines the minimum distance between two points that can be distinguished, based on the wavelength of light used and the numerical aperture of the lens system.
This formula was developed by Ernst Abbe, a prominent physicist in the 19th century, who greatly contributed to the understanding of optical systems.
The formula incorporates important factors such as the refractive index of the medium and the wavelength of light. By understanding these elements, researchers can optimize their optical setups for better clarity and detail in microscopic imaging.
This capability is essential in fields like biology and materials science, where observing small details can be critical for advancements.
As scientific exploration continues to push boundaries, mastering Abbe’s formula offers valuable insights into the limitations and potential of modern microscopy. With this knowledge, scientists can enhance their techniques and uncover new discoveries.
Optical Theory Behind Abbe’s Formula

Abbe’s formula is rooted in essential concepts of optics, including refractive index, numerical aperture, and diffraction. These principles help explain how light behaves in microscopes, impacting resolution and the limits of imaging.
Understanding Refractive Index
The refractive index is a key factor in optics, measuring how much light bends when passing through a material. Each optical material, such as glass, has its specific refractive index. A higher refractive index indicates that light slows down more as it enters the material, which can improve resolution in microscopy.
Abbe’s formula relates this property to the resolution limit of optical systems. When light travels between different mediums, such as air and glass, the change in speed causes distortion. This can lead to optical aberrations, which negatively affect image quality and sharpness.
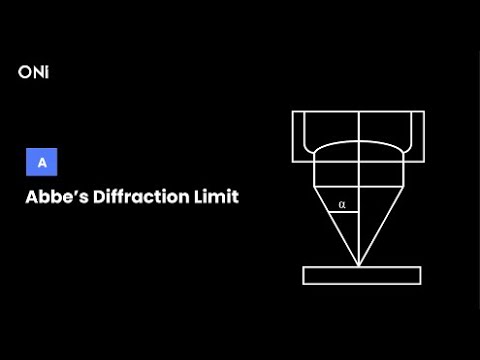
Concept of Numerical Aperture
Numerical aperture (NA) describes a microscope’s ability to gather light and resolve fine detail at a fixed distance. NA is defined as the sine of the maximum half-angle of the cone of light that can enter or exit the lens, multiplied by the refractive index of the medium.
A higher NA value means better light-gathering ability and finer resolution capability. As NA increases, it improves the resolving power according to the Rayleigh criterion. This criterion determines the minimum distance between two points that can be distinguished as separate. Therefore, numerical aperture is crucial for achieving optimal imaging in microscopy.
Diffraction and Resolution Limits
Diffraction occurs when light waves encounter obstacles or openings. This phenomenon can limit the resolution of optical systems. According to Abbe’s theory, the diffraction limit is the point where the resolving power reaches its maximum based on the system’s design.
The resolution limit can be increased by minimizing the effects of diffraction. Techniques such as using higher NA lenses and optimizing light wavelength can help improve the clarity of images. Understanding diffraction is vital for developing advanced imaging techniques that push the boundaries of traditional microscopy.
Wavelength of Light in Microscopy
The wavelength of light significantly influences imaging capabilities. Shorter wavelengths, like blue light, yield higher resolution compared to longer wavelengths, such as red light. Abbe established that the resolution limit is directly related to the wavelength used in microscopy.
Using the formula derived from Abbe’s work, it is possible to calculate the minimum resolvable distance. This emphasizes the importance of selecting the appropriate wavelength to achieve clear and detailed images. By considering wavelength along with refractive index and numerical aperture, researchers can enhance the performance of optical systems.
Abbe’s Formula In Practice

Abbe’s formula plays a critical role in optical design, especially in microscopy and imaging systems. Understanding its practical application aids in achieving desired resolution, minimizing chromatic aberration, and optimizing optical components.
Role in Microscope Design
Abbe’s formula is foundational in the design of optical microscopes. It defines the relationship between the refractive index of a material and its dispersive power. The Abbe number (V-number) helps to determine how much light is separated into different wavelengths when passing through optical glass.
This is crucial in designing objective lenses and condensers used in microscopes. Higher Abbe values indicate better performance in reducing chromatic aberration. When designing these systems, manufacturers must choose materials with suitable Abbe numbers to ensure clear and accurate imaging.
Importance for Imaging Systems
In imaging systems, Abbe’s formula is vital for achieving high-resolution images. The Abbe diffraction limit indicates the smallest detail that can be resolved based on the optical setup. This limit is influenced by the numerical aperture (NA) of the system, which accounts for the light-gathering ability of the lens.
By optimizing the NA and using lenses with appropriate Abbe values, imaging systems can effectively reduce the size of the airy disc, thus enhancing clarity. This plays an essential role in fields like biomedical imaging and materials science, where precision is critical.
Factors Affecting Resolution
Several factors influence the resolution in optical systems, largely governed by Abbe’s principles. The refractive index of the optical materials used directly impacts image sharpness. Lenses with higher refractive indices usually enable greater numerical apertures, which in turn increases resolution.
Additionally, chromatic aberration must be minimized, as it can distort colors and detail. Using lenses designed according to the Abbe formula helps correct these issues. The interplay between axial resolution and lateral resolution must also be considered, ensuring that both in-focus detail and overall image quality are achieved.
Adjustments for Axial and Lateral Resolution
Achieving optimal axial and lateral resolution requires careful adjustments based on the principles outlined by Abbe. Axial resolution refers to the ability to distinguish details along the optical axis, while lateral resolution deals with details across the field of view.
These resolutions can often be improved by manipulating the numerical aperture and using specific configurations of optical lenses. The point spread function describes how a point of light is spread out in an image, affecting both resolutions.
In practice, understanding the relationship between the Abbe number, NA, and point spread function helps in fine-tuning optical performance. These adjustments are essential for producing high-quality images across various applications in microscopy and imaging systems, including those used in microscopes.
Advancements and Limitations
Advancements in microscopy have led to significant improvements in spatial resolution, but challenges remain. Understanding both the benefits and drawbacks of Abbe’s formula is crucial for researchers and practitioners.
Beyond the Diffraction Limit
The diffraction limit, described by Abbe’s formula, sets a theoretical boundary for spatial resolution in optical microscopy. New methods have emerged to surpass this boundary. For example, structured illumination enhances resolution by manipulating light patterns. Techniques like stimulated emission depletion (STED) microscopy also push beyond this limit by selectively turning off fluorescence from specific areas.
These advancements allow scientists to view structures much smaller than the diffraction limit of light. Electron microscopy presents another leap forward. It utilizes electron beams instead of light, achieving resolutions as fine as a few nanometers. This method enables the observation of intricate cellular components.
Materials and Optical Performance
The choice of materials affects the performance of optical systems significantly. Achromatic lenses, made with multiple types of glass, minimize chromatic aberration, improving image clarity. The numerical aperture (NA) of a lens is critical for determining resolution. Higher NA values yield better performance in resolving closely spaced objects.
Advances in coating technologies also enhance the transmission of light through lenses. Anti-reflective coatings reduce light loss, optimizing optical performance. However, the limitations of materials can introduce distortions. Hence, researchers constantly explore new materials and designs to improve the capabilities of optical systems.
Cutting-Edge Techniques and Achievements
Recent achievements in microscopy illustrate dramatic improvements in resolution and imaging speed.
Laser beams tightly focused using adaptive optics can generate clearer images without significant distortion. These techniques analyze and correct wavefront errors, producing more accurate data.
Furthermore, innovations such as super-resolution microscopy allow for imaging at resolutions previously deemed impossible.
By utilizing advanced algorithms and hardware, this technology enables scientists to visualize complex biological processes in real time.
Researchers continue to push the boundaries of what is possible with microscopy, emphasizing the importance of adapting to limitations while exploring new avenues for discovery.

