Light behaves in fascinating ways as it travels through different media. When light strikes a boundary between two materials, it can either reflect off the surface or refract, bending as it passes through.
The angle of incidence is not equal to the angle of refraction. Instead, the relationship between them is defined by the law of refraction, also known as Snell’s Law.
In simple terms, the angle of incidence is the angle at which incoming light strikes a surface, while the angle of refraction is the angle at which light bends when it enters a new medium.
Refraction occurs because light travels at different speeds in different substances. This difference in speed causes the light to change direction, leading to a clear relationship between the angles involved.
Understanding this concept is key not only in optics but also in practical applications like designing lenses and predicting how light behaves in everyday situations, such as when viewing objects underwater. Exploring the nature of angles in refraction reveals much about how we perceive the world around us.
Fundamentals of Light and Refraction

Light plays a crucial role in optics, influencing how we perceive the world. Understanding its nature and the process of refraction is essential in various applications.
Nature of Light
Light is a form of electromagnetic radiation visible to the human eye. It behaves both as a particle and a wave, which is fundamental in optics.
Light travels in straight lines known as rays. The speed of light varies depending on the medium. In a vacuum, it travels at approximately 299,792 kilometers per second.
When light enters a different medium, like water or glass, its speed decreases due to the medium’s refractive index.
The refractive index measures how much light bends when entering a new medium. A higher refractive index indicates light will slow down more compared to a medium with a lower refractive index. This property of light is essential in creating lenses and optical devices.
Understanding Refraction
Refraction is the bending of light as it passes from one medium to another. This change in speed causes light to alter its direction. Snell’s Law mathematically describes this phenomenon, stating that the ratio of the sine of the angle of incidence (the angle the incoming ray makes with the normal) to the sine of the angle of refraction (the angle the outgoing ray makes with the normal) equals the ratio of the refractive indices of the two media.
This relationship helps predict how much light will bend when entering a new material. For example, when light travels from air (lower refractive index) to water (higher refractive index), it slows down and bends towards the normal line, making the angle of refraction less than the angle of incidence.
Interplay Between Incidence and Refraction
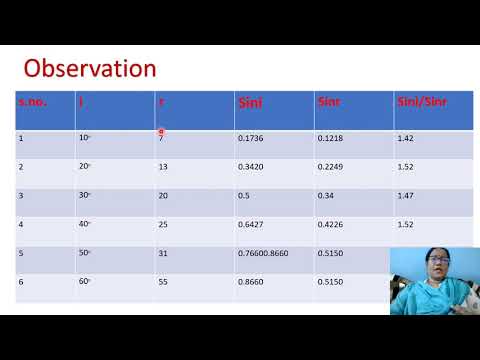
The interaction between the angle of incidence and the angle of refraction is crucial in understanding how light behaves as it transitions between different media. The principles governing these angles explain phenomena such as how lenses focus light and the conditions required for total internal reflection.
Exploring Snell’s Law
Snell’s Law describes the relationship between the angle of incidence and the angle of refraction when light moves between two media. It is mathematically expressed as:
n1 * sin(θ1) = n2 * sin(θ2)
In this equation, n1 and n2 are the refractive indices of the two media, while θ1 is the angle of incidence and θ2 is the angle of refraction.
When light travels from a less dense medium (like air) to a denser one (like water), the angle of refraction decreases, bending the light toward the normal line. Conversely, moving from denser to less dense results in an increase in the angle of refraction. This behavior is fundamental in applications such as fiber optics, where precise control of light paths is essential.
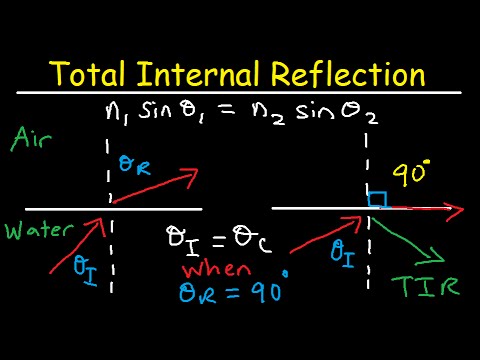
Critical Angle and Total Internal Reflection
The concept of the critical angle plays a significant role in optics. The critical angle is the angle of incidence above which total internal reflection occurs. This phenomenon can be observed when light travels from a denser medium to a less dense one, like water to air.
If the angle of incidence exceeds the critical angle, all the incident light is reflected back rather than refracting. This phenomenon is utilized in optical fibers, ensuring efficient light transmission.
The critical angle can be calculated using the formula:
sin(θc) = n2/n1
Where θc is the critical angle, and n1 and n2 are the refractive indices of the respective media.
Applications of Refraction in Optics
Refraction plays a crucial role in optics, impacting how light behaves and is utilized in various technologies. This section covers how lenses utilize refraction and its implications in modern communication technology.
Refraction in Lenses
Lenses are essential optical devices that manipulate light through refraction. They bend light to focus or disperse rays, depending on their shape and materials. The refractive index of a lens material determines how much the light will bend.
Convex lenses, for instance, converge light rays to a focal point. This property is valuable in devices like microscopes and telescopes, enhancing visibility of distant or tiny objects.
In contrast, concave lenses diverge light rays and are used in applications like eyeglasses.
The wavelength of light influences how it refracts as well. Different colors of light bend at various angles when passing through a lens. This phenomenon, known as chromatic aberration, can affect image clarity. High-quality lenses are designed to minimize these distortions.
Technological Implications of Refraction
Refraction extends beyond traditional optics to modern technologies like fiber optics.
These systems use light to transmit data over long distances with minimal loss.
The refractive index of the fiber material is crucial for guiding light effectively.
In fiber optics, the principle of total internal reflection relies on the refractive index difference between the fiber and surrounding materials.
This ensures signals remain clear and strong, which is vital for communication technology.
Refraction is also important in developing devices like binoculars and spotting scopes.
These tools rely on precise lens shapes to enhance vision.
Manufacturers utilize the principles of refraction to create optics that provide sharp images and a wide field of view.
By leveraging the science of refraction, advancements in optics continue to evolve, greatly impacting technology and daily life.

