To find the angle of incidence, one must first understand its definition in the study of optics. The angle of incidence is the angle formed between an incoming light ray and an imaginary line known as the normal, which is perpendicular to the surface at the point of contact.
This angle is crucial because it directly affects how light behaves when it encounters different materials, influencing both reflection and refraction.
When light travels from one medium to another, such as from air into water, the refractive index of each medium plays a key role.
Depending on the angle at which the light strikes the surface, it may either reflect back into the original medium or pass through into the new one at a different angle.
Understanding how to determine the angle of incidence allows one to predict these behaviors accurately, making it essential in applications ranging from photography to optical engineering.
By using simple geometric principles, anyone can calculate the angle of incidence. Tools such as protractors or angle finders can be useful when measuring directly.
With a clearer grasp of the concept, readers can delve into practical examples and common scenarios where finding the angle of incidence is vital.
Understanding Incident Angle and Refraction

The incident angle is a key concept in optics that affects how light behaves when it encounters different materials. This section explores the specifics of the angle of incidence and the principles of refraction, including how they relate to Snell’s Law and the refractive index.
Defining Angle of Incidence
The angle of incidence is the measure of the angle between an incoming light ray and the normal line, which is an imaginary line perpendicular to the surface at the point of incidence. This angle plays a crucial role in determining how light interacts with various materials.
When light travels through air and strikes a different medium, such as water or glass, the angle of incidence helps define the angle at which the light will then refract.
According to Snell’s Law, the relationship between the angle of incidence and the angle of refraction depends on the refractive indices of the involved materials.
Basics of Refraction
Refraction occurs when light passes through different media and bends due to a change in speed. This change in speed is a result of the refractive index of the materials involved.
The refractive index indicates how much light slows down in a medium compared to air.
The relationship can be described by Snell’s Law:
n₁ * sin(θ₁) = n₂ * sin(θ₂)
Where:
- n₁ = refractive index of the first medium
- θ₁ = angle of incidence
- n₂ = refractive index of the second medium
- θ₂ = angle of refraction
Understanding this law is essential for predicting how light will behave when entering a new medium, such as when light moves from air into water. This knowledge is applied in various fields, including optics, photography, and even sports like swimming.
Determining Incident Angle Using Snell’s Law
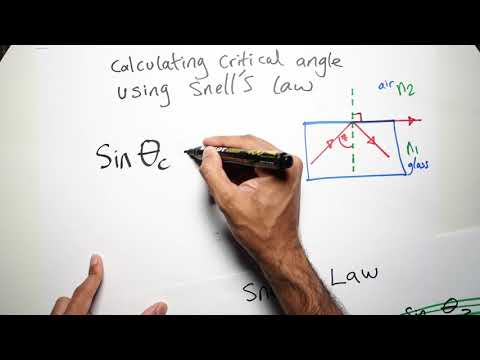
Snell’s Law provides a precise method for calculating the angle of incidence when light transitions between different mediums. Understanding how to apply this law is essential for various applications in optics.
Mathematical Expression of Snell’s Law
Snell’s Law can be expressed with the equation:
n₁ * sin(θ₁) = n₂ * sin(θ₂)
In this formula, n₁ and n₂ represent the refractive indices of the two media. θ₁ is the angle of incidence, while θ₂ is the angle of refraction.
When light hits a surface, the incident ray approaches at an angle. By rearranging the equation, the angle of incidence can be isolated:
θ₁ = arcsin((n₂ / n₁) * sin(θ₂))
This rearrangement allows a person to determine the angle of incidence when the refractive indices and angle of refraction are known. Utilizing a scientific calculator makes this calculation straightforward.
Refractive Index Relationship
The refractive index indicates how fast light travels in a medium compared to air. Air has a refractive index of approximately 1.00, while glass typically has a refractive index around 1.52.
This index affects how much the light ray bends at the interface between two media. For example, when light moves from air into glass:
- The angle of incidence (θ₁) is measured from the normal line.
- The angle of refraction (θ₂) occurs as the ray enters the glass.
To find the incident angle accurately, knowing both refractive indices is vital. This relationship plays a key role in various fields, including photography and fiber optics, where precise light manipulation is essential.
Experimental Methods to Find the Incident Angle

Finding the incident angle is essential in optics. Several experimental methods help determine this angle accurately, using different techniques such as mirror reflection, measurement of refractive indices, and advanced spectroscopy methods.
Using a Plane Mirror
One straightforward method to find the angle of incidence involves a plane mirror. When a light ray strikes the mirror, it reflects according to the law of reflection. This states that the angle of incidence equals the angle of reflection.
To measure these angles, an experimental setup with a protractor can be used.
- Setup: Position the plane mirror on a flat surface.
- Light Source: Use a laser pointer or flashlight to direct a beam towards the mirror.
- Measurement: Use the protractor to measure the angle between the incident ray and the normal line at the point of incidence.
This method is simple but effective for educational demonstrations and basic physics experiments.
Refractive Index Measurement Techniques
Another way to determine the incident angle is through refractive index measurement. This method often employs a prism to explore how light bends as it enters a new medium. The index of refraction is essential in predicting how much light will deviate based on the angle of incidence.
In this procedure:
- Prism Setup: Place a prism on a flat surface.
- Light Entry: Shine a coherent light source at various angles toward the prism.
- Data Collection: Measure the angles of incidence and refraction using a protractor.
Using Snell’s Law, which relates the angles and indices of refraction, the incident angle can be calculated. This technique is vital in fields such as optical engineering and telecommunications.
Atom Optics and X-ray Spectroscopy
Advanced techniques like atom optics and X-ray spectroscopy provide precise methods for finding incident angles, especially in research settings. Grazing incidence diffraction experiments are useful for studying surface structures.
In these methods:
- X-ray Setup: Direct X-rays at a sample surface at a low angle.
- Measurement Techniques: Analyze the diffraction pattern to determine the incident angle.
- Data Interpretation: The angles can reveal details about atomic arrangements in materials like diamonds.
These experimental setups are more complex but are pivotal in advancing materials science and nanotechnology. The application of these methods can lead to significant advancements in understanding material properties and behaviors.
Practical Applications and Considerations

Finding the incident angle is important in various fields, including optics and engineering.
Understanding this angle helps in designing effective optical devices.
Total internal reflection occurs when light hits a boundary at an angle greater than the critical angle. This principle is significant in fiber optics, where light must stay within the core of the fiber.
The critical angle varies based on the materials involved, particularly their refractive indices.
For example, in air, the refractive index is approximately 1.00. When light enters a medium with a higher refractive index, such as glass, the incident angle affects the amount of light reflected versus refracted.
Consider telescopes and binoculars. These devices rely on precise angles to gather and focus light.
Adjusting the incident angle can improve the clarity of the image one sees. Spotting scopes also benefit from understanding how light behaves at different angles, affecting target visibility.
When measuring angles, using appropriate tools like protractors or software can ensure accuracy.
Small errors in angle measurement can lead to significant differences in performance.
In applications related to imaging and visuals, comprehension of angles enables improved designs.
Whether in a professional setting or recreational use, mastering the incident angle leads to better optics and enhanced experiences.

