When light travels from one medium to another, it bends in a specific way. An example of Snell’s law is when light passes from air into water. This causes it to change direction based on the angle of incidence and the angle of refraction. This phenomenon demonstrates how light refracts, or bends, as it enters a new medium, influenced by the different properties of each substance.
Understanding Snell’s law is essential in optics. The law provides a formula that relates the angles of incidence and refraction to the refractive indices of the two media involved. This relationship not only helps explain everyday occurrences, like the bending of a straw appearing broken in a glass of water, but it also has important applications in various technologies, from glasses to cameras.
By grasping these concepts, readers can appreciate the science behind why things look different in water compared to air. Snell’s law connects simple observations to deeper principles in physics, making it a key topic in the study of light and optics.
Fundamentals of Snell’s Law
Snell’s Law describes how light bends when it travels between different media, such as air and water. Understanding the basics involves knowing refractive indices and the behavior of incident and refracted rays.
Understanding Refractive Indices
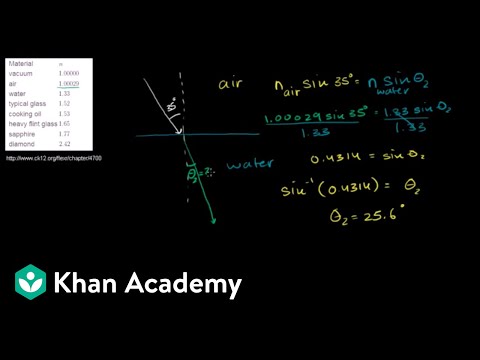
The refractive index is a crucial concept that measures how much light slows down in a medium compared to air. For instance, the refractive index of air is approximately 1.00, while water has a higher refractive index of about 1.33.
This means light travels slower in water than in air. The higher the refractive index, the more the light bends when it passes from air into that medium. When calculating the angles of incidence and refraction, it is essential to know these indices, as they determine how much light will bend at the boundary between two different materials.
The Role of the Incident and Refracted Rays
In optics, the incident ray is the incoming light that strikes the boundary between the two media. The refracted ray is the light that exits into the second medium.
Both rays interact with a line called the normal, which runs perpendicular to the boundary surface at the point of incidence. The angle of incidence is formed between the incident ray and the normal line, while the angle of refraction is between the refracted ray and the normal.
Understanding this relationship between the incident and refracted rays is essential for applying Snell’s Law in real-world scenarios like designing lenses or understanding how eyeglasses correct vision.
Angles and Their Measurements
The angles in Snell’s Law are measured in degrees, often using a protractor for accuracy. The angle of incidence is the angle between the incident ray and the normal line. The angle of refraction is the angle between the refracted ray and the normal.
Snell’s Law expresses the relationship between these angles and the refractive indices of the two media involved. The formula can be written as:
[ n_1 \cdot \sin(\theta_1) = n_2 \cdot \sin(\theta_2) ]
In this equation, ( n_1 ) and ( n_2 ) are the refractive indices, while ( \theta_1 ) and ( \theta_2 ) are the angles of incidence and refraction, respectively. This relationship explains how varying angles and media impact the path of light.
Mathematical Formulation of Snell’s Law

Snell’s Law provides a mathematical framework to understand how light behaves when it passes between different media. The relationship involves angles of incidence and refraction, as well as the refractive indices of the materials involved. Understanding this formulation is essential in various applications like lens design and optical devices.
Calculating Angles of Incidence and Refraction
The mathematical equation for Snell’s Law is given by:
n₁ sin(θ₁) = n₂ sin(θ₂)
Here, n₁ and n₂ are the refractive indices of the respective media. θ₁ represents the angle of incidence, while θ₂ is the angle of refraction.
To calculate these angles, one rearranges the equation:
θ₂ = arcsin((n₁/n₂) sin(θ₁))
This equation shows how the angle of light changes as it moves from one medium to another. The refractive index indicates how much the speed of light decreases in a medium compared to a vacuum.
Relationship Between Speed and Wavelength
Light travels at different speeds in different media, defined by the refractive index. The speed of light in a medium is v = c/n, where c is the speed of light in a vacuum.
The wavelength (λ) is also affected by the media. The relationship can be expressed as:
λ₂ = (v/f)
where f is the frequency of the light. As light enters a medium with a higher refractive index (slower speed), its wavelength decreases in proportion to the refractive index. Understanding these relationships helps in designing optical systems that utilize lenses and fibers effectively.
Applications of Snell’s Law

Snell’s Law plays a vital role in many areas of science and technology. From designing advanced optical instruments to enhancing telecommunications, its applications are extensive. This section explores how Snell’s Law is utilized in various fields, including the design of optical instruments, advancements in telecommunications, and understanding natural phenomena.
Design of Optical Instruments
Snell’s Law is fundamental in the creation of various optical instruments like microscopes, telescopes, and cameras. The law governs how light refracts as it enters different materials.
For instance, in the design of lenses, the correct curvature and material are crucial to focus light accurately. Lenses in eyeglasses are designed based on Snell’s Law to correct vision by bending light to the retina. Devices such as microscopes use lenses to magnify small objects by applying the principles of refraction.
Additionally, the law is used in creating spotting scopes and binoculars, ensuring that they deliver clear images by minimizing distortions. By ensuring light travels efficiently through these optical components, Snell’s Law helps provide precise and sharp visuals.
Advancements in Telecommunications
Snell’s Law is also essential in telecommunications, particularly in the use of fiber optics. Fiber optic cables rely on total internal reflection, which is a consequence of Snell’s Law. When light travels through the fiber at a certain angle, it reflects entirely within the cable, allowing data to be transmitted over long distances without loss.
This technology is crucial for internet and telephone services. By optimizing light transmission in fiber optic cables, telecommunications companies can provide faster data transfer rates. The knowledge of Snell’s Law ensures that these systems are designed efficiently, improving connectivity and communication.
Understanding Natural Phenomena
Snell’s Law helps explain various natural phenomena, including the formation of rainbows.
When light passes through water droplets in the atmosphere, it refracts and reflects, creating a spectrum of colors. This effect is a direct application of the principles defined by Snell’s Law.
Additionally, it can explain why objects appear distorted when viewed underwater.
As light travels from air to water, it bends, altering the perceived position of submerged objects.
By understanding this bending of light, one gains insight into many optical phenomena seen in nature.

