Calculating Snell’s Law is essential for understanding how light behaves when it passes through different materials. This fundamental principle in optics explains how the light bends at the boundary between two media.
To calculate Snell’s Law, one can use the formula: n1 × sin(θ1) = n2 × sin(θ2), where n represents the refractive index, θ1 is the incident angle, and θ2 is the angle of refraction.
When light enters a new medium, the change in speed causes it to bend. The incident angle, the angle at which the light hits the surface, plays a crucial role in determining the angle of refraction.
Understanding these angles helps in various applications, from lens design to understanding how we see images through water or glass.
Engaging with Snell’s Law reveals how light interacts with the world around us. This fascinating concept not only underpins many optical devices but also enriches our understanding of everyday phenomena, such as why a straw looks bent in a glass of water.
Fundamentals of Refraction and Snell’s Law

Refraction is the bending of light as it passes through different media. This phenomenon occurs due to changes in speed as light moves between materials. Understanding this bending is crucial for calculating Snell’s Law, which relates the angles of incidence and refraction to the refractive index of the materials involved.
Exploring the Concept of Light Refraction
Refraction happens when a light ray crosses the boundary between two different materials, such as air and water. As the light ray enters a new medium, its speed changes, causing it to bend. This bending occurs at a specific angle called the angle of incidence, which is the angle between the incoming ray and the normal line (an imaginary line perpendicular to the surface).
The angle of refraction is the angle between the refracted ray and the normal line. To visualize this, consider a straight straw in a glass of water; it appears bent at the surface due to light refraction.
Understanding how light interacts with different materials helps in various applications, from designing glasses to developing optical instruments. More information can be found in related articles.
Understanding Snell’s Law of Refraction
Snell’s Law provides a formula to predict the angles of incidence and refraction. It states that the ratio of the sine of the angle of incidence (θ₁) to the sine of the angle of refraction (θ₂) is equal to the ratio of the refractive indices of the two media (n₁ and n₂). The formula is expressed as:
[ n₁ \sin(θ₁) = n₂ \sin(θ₂) ]
Here, n₁ is the refractive index of the first medium, and n₂ is that of the second. This law helps in calculating how much a light ray will bend when entering a new medium, making it essential for optics. When light travels from air (which has a refractive index of about 1) into water (approximately 1.33), Snell’s Law can be easily applied using these values.
Calculating the Index of Refraction
The refractive index is a measure of how much light slows down in a medium compared to its speed in a vacuum. It is calculated using the formula:
[ n = \frac{c}{v} ]
In this formula, n is the refractive index, c is the speed of light in a vacuum (approximately 3 x 10^8 m/s), and v is the speed of light in the medium. For example, if light travels through glass at about 2 x 10^8 m/s, the refractive index would be:
[ n = \frac{3 x 10^8}{2 x 10^8} = 1.5 ]
This value indicates that light travels slower in glass than in a vacuum. Understanding and calculating the refractive index is crucial for applications ranging from fiber optics to camera lenses.
Applying Snell’s Law

Applying Snell’s Law involves practical methods to calculate angles of refraction, the use of the refractive index, and understanding how different materials affect light. This knowledge is essential for anyone interested in optics.
Calculating Angles of Refraction
To calculate the angle of refraction, one must use Snell’s Law, expressed mathematically as:
[ n_1 \sin(\theta_1) = n_2 \sin(\theta_2) ]
In this equation, ( n_1 ) and ( n_2 ) represent the indices of refraction for two different media. The angle of incidence (( \theta_1 )) is the angle at which light hits the boundary, while the angle of refraction (( \theta_2 )) is the angle at which it travels in the new medium.
To find the angle of refraction, rearrange the equation as follows:
[ \sin(\theta_2) = \frac{n_1 \sin(\theta_1)}{n_2} ]
By substituting known values, a calculator can quickly determine ( \theta_2 ). This method is widely used in various applications ranging from eyeglasses to camera lenses.
Using Refractive Index in Calculations
The refractive index is a crucial value in determining how light behaves in different materials. Common indices of refraction include:
- Air: 1.0003
- Water: 1.33
- Glass: 1.5
Knowing these values allows for accurate calculations when light transitions from one medium to another. For example, when light travels from air into glass, the change in speed causes refraction. Using an Index of Refraction Calculator, one can quickly input the angles and indices to efficiently find unknown values.
This practical application of refractive indices helps in designing optical devices like lenses and fiber optics.
Differences in Refraction by Medium
The degree of refraction varies between materials due to their differing refractive indices. For instance, light bends more when moving from air into water compared to moving from air into glass.
This difference is crucial for understanding how lenses focus light. In optics, a higher refractive index means a greater change in angle for the same angle of incidence. Recognizing these differences enables precise control over light paths, which can enhance clarity and focus in optical systems.
This knowledge is essential for tasks such as designing lenses used in photography or telescopes. Understanding each material’s impact on light helps in effectively manipulating optical phenomena.
Snell’s Law and Optical Phenomena

Snell’s Law plays a critical role in understanding various optical phenomena. This section explores key concepts, such as total internal reflection, the critical angle, and how the wavelength of light affects refraction.
Understanding Total Internal Reflection
Total internal reflection occurs when light attempts to move from a denser medium to a less dense one at a steep angle. If the angle exceeds a specific threshold, known as the critical angle, all the light reflects back into the denser medium instead of refracting.
This phenomenon is essential in fiber optics and certain types of lenses. For example, optical fibers use total internal reflection to transmit light effectively. The light remains trapped within the fiber core, allowing it to travel long distances without significant loss.
Identifying the Critical Angle
The critical angle is the angle of incidence that results in an angle of refraction of 90 degrees. This means that beyond this angle, light will not exit the denser medium. The critical angle can be calculated using the formula:
Critical Angle Formula:
[ \text{Critical Angle} (\theta_c) = \sin^{-1}\left(\frac{n_2}{n_1}\right) ]
Where ( n_1 ) is the refractive index of the denser medium and ( n_2 ) is that of the less dense medium. For example, when light travels from glass (n ≈ 1.5) to air (n ≈ 1.0), the critical angle is approximately 41 degrees. This knowledge is crucial in designing optical instruments.
Impact of Wavelength on Refraction
The wavelength of light affects how it bends when passing through different media. Different wavelengths experience different refractive indices, meaning they will bend at varying angles. This variation leads to the phenomenon of dispersion, where white light separates into its constituent colors, as seen in rainbows.
Shorter wavelengths (like blue light) refract more than longer wavelengths (like red light). This difference is significant in applications such as prisms and lenses, influencing how images are focused or how colors are displayed in various technologies.
Practical Applications and Calculators
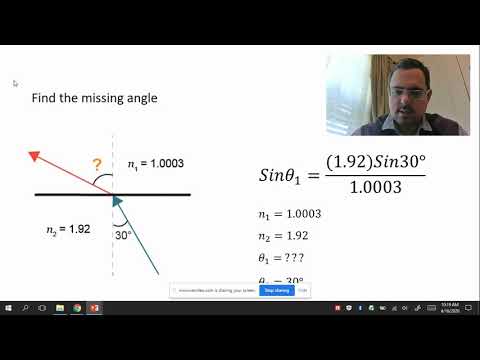
Understanding Snell’s Law is crucial for various fields. This law helps calculate how light bends when it passes through different materials. Using calculators can simplify this process.
Using a Snell’s Law Calculator
A Snell’s Law Calculator allows users to quickly determine the angle of refraction when light transitions between two media. To use it, one must input the refractive indices of both materials. For example, if light moves from air to Plexiglas, the indices of refraction come into play.
Most online calculators, like those available on various educational sites, provide a user-friendly interface. They usually require only the angles of incidence and the indices of refraction. This makes calculations straightforward, even for complex optics problems.
Additionally, these calculators often provide visual representations of the light beam’s path. This aids in visual learning, making Snell’s Law easier to grasp.
Applications in Optics and Engineering
Snell’s Law finds extensive applications in optics and engineering.
It is essential in designing lenses for devices like microscopes and telescopes.
Understanding light behavior is crucial for creating efficient optical instruments.
In engineering, Snell’s Law helps in selecting materials for various applications, including coatings that minimize reflection.
For instance, anti-reflective coatings are common in glasses and camera lenses.
Furthermore, knowledge of refraction is vital in fields that require precise alignment of light beams, such as fiber optics.
Accurate calculations ensure optimal performance in technologies that rely on focused light.

